One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘
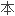
 研究了四元数量子力学中一类
研究了四元数量子力学中一类 求其解是正规或可对角化四元数矩阵的特征值反问题。
求其解是正规或可对角化四元数矩阵的特征值反问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。