As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-
K_1- 与其边界上
与其边界上 上同伦
上同伦 同构。
同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,我们证明了作为泛代数 半格
半格 定义与作为偏序集
定义与作为偏序集 半格
半格 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李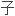

 性质得出了李
性质得出了李
 两个李
两个李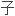

 交依然是李
交依然是李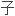

 结论,进而得出这一李
结论,进而得出这一李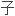

 李代数形式。
李代数形式。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积
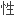
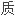
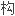 造了一个3 维
造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-群与其边界上
K_1-群与其边界上 上同伦群同
上同伦群同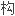 。
。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,我们证明了作为泛代数
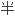
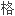
 定义与作为偏序集
定义与作为偏序集
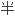
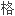
 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李子群
 得出了李群
得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以上例句、词 分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件
分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,
 有
有 域
域 拓扑
拓扑

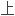 连续函数代数
连续函数代数 K_1-群与其
K_1-群与其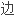

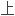

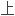 同伦群同构。
同伦群同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,我们证明了作为泛代数 半格
半格 定义与作为偏序集
定义与作为偏序集 半格
半格 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李子群 性质得出了李群
性质得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以 例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件
例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由
loop代数 ,由

 计出许多新
计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-群与其边界上
K_1-群与其边界上 上同伦群同构。
上同伦群同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,我们证明了作为泛代数
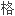
 定义与作为偏序集
定义与作为偏序集
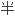
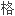
 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李子群 性质得出了李群
性质得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱
等谱
 ,
,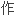 为应用,本文得到了一个类似
为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-群与其边界上
K_1-群与其边界上 上同伦群同构。
上同伦群同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,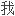
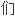
 明了
明了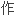 为泛代数
为泛代数 半格
半格 定义与
定义与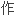 为偏序集
为偏序集 半格
半格 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李子群 性质得出了李群
性质得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现
观点;若发现
 ,欢迎向
,欢迎向
 指正。
指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积
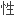
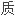
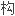 造了一个3 维
造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-群与其边界上
K_1-群与其边界上 上同伦群同
上同伦群同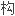 。
。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,我们证明了作为泛代数
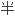
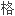
 定义与作为偏序集
定义与作为偏序集
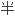
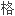
 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李子群
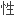
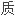 得出了李群
得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以上例句、词 分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件
分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,
等谱问题,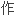
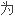
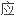 用,本
用,本 得到了一个类似
得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C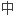 ,任意有界域
,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-群与其边界上
K_1-群与其边界上 上同伦群同构。
上同伦群同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本
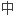 ,
,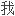 们证明了
们证明了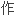
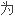 泛代数
泛代数 半格
半格 定义与
定义与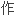
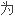 偏序集
偏序集 半格
半格 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
 章通过李子群
章通过李子群 性质得出了李群
性质得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向
观点;若发现问题,欢迎向 们指正。
们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.
最后利用外积 性质构造了一个3 维
性质构造了一个3 维 loop
loop
 ,由此可设计出许多新
,由此可设计出许多新 等谱问题,作为应用,本文得到了一个类似
等谱问题,作为应用,本文得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)
Boite-Pempinelli-Tu(BPT) 。
。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
 复平面C中,任意有界域
复平面C中,任意有界域 拓扑边界上连续函
拓扑边界上连续函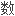
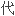
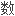
 K_1-群与其边界上
K_1-群与其边界上 上同伦群同构。
上同伦群同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本文中,我们证明了作为泛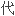
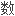
 半格
半格 定义与作为偏序集
定义与作为偏序集 半格
半格 定义是等价
定义是等价 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
文章通过李子群 性质得出了李群
性质得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李
李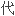
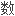 形式。
形式。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不 表本软件
表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
As its application, a multi-component system similar to the BPT hierarchy is obtained.


 用外积
用外积 性质构造了一个3 维
性质构造了一个3 维 loop代数 ,由此可设计出许多新
loop代数 ,由此可设计出许多新 等谱问题,作为应用,本
等谱问题,作为应用,本 得到了一个类似
得到了一个类似 多分量
多分量 Boite-Pempinelli-Tu(BPT)族。
Boite-Pempinelli-Tu(BPT)族。
Further more,we prove that the cohomotopy groups is isomorphic to K1 -group of the continuous algebra on topological boundary of bounded domains in C.
在复平面C中,任意有界域 拓扑边界上连续函数代数
拓扑边界上连续函数代数 K_1-群与其边界上
K_1-群与其边界上 上同伦群同构。
上同伦群同构。
In this paper, we proved that the definition of a semilattice as a universal algebra and the definition of a semilattice as a partial ordered set are equivalent.
本 中,我们证明了作为泛代数
中,我们证明了作为泛代数 半格
半格 定义与作为偏序集
定义与作为偏序集 半格
半格 定义是等
定义是等
 。
。
In this paper, the conclusion is that the intersection of lie subring of a Lie group is a Lie subring is obtained, moreover,it gives the Lie algebra of the Lie subring.
 章通过李子群
章通过李子群 性质得出了李群
性质得出了李群 两个李子群
两个李子群 交依然是李子群
交依然是李子群 结论,进而得出这一李子群
结论,进而得出这一李子群 李代数形式。
李代数形式。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。