According to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根
双调和方程的特点并借助于MATHEMATICA软件,得到了应力函数双调和方程的多项式解
。
diào hé de
conciliatory, consistent, consonant, symphonious声明：以上例句、词性分类均由互联网资源自动生成，部分未经过人工审核，其
容亦不代本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
grissino, grist, grist mill, gristcase, gristle, gristly, gristmill, grists, grit, gritcrete,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据二维双调和方
特点并借助于MATHEMATICA软件,得到了应力函数双调和方
项式解。
声明：以
、词性分类均由互联网资源自动生成，部分未经过人工审核，其表达内容亦不代表本软件
观点；若发现问题，欢迎向我们指正。
用户正在搜索
grizzly, grizzly bear, grizzlyman, GRM, GRO, groan, groaning, groans, groat, groatcake,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
据二维双调和方程的特点并借助于MATHEMATICA软件,得到了应力函数双调和方程的多项式解。
声明：以上例、词性分类均由互联网资源自动生成，部分未经过人工审核，其表达内
代表本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
Groeberiidae, Groenendael, grog, groggery, groggily, groggy, grogram, grogshop, groid, groin,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据二维双
程的特点并借助于MATHEMATICA软件,得到了应力函数双程的多项式解。
声明：以上例句、词
类均由互联网资源自动生成，部未经过人工审核，其表达内容亦不代表本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
grooming, groomsman, groove, grooveability, grooved, groovelike, groover, groovine, grooving, groovox,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据二维双调和方程的特点
助于MATHEMATICA软件,得到了应力函数双调和方程的多项式解。
声明：以上例句、词性类均由互联网资源自动生
，
未经过人工审核，其表达内容亦不代表本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
groschen, grosgrain, gross, gross anatomy, gross domestic product, gross margin, gross national product, gross profit, gross profit margin, gross revenue,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据二维双调和方程的特点并借助于MATHEMATICA软件,得到了应力函数双调和方程的多
。
：
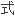
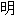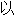上例句、词性分类均由互联网资源自动生成，部分未经过人工审核，其表达内容亦不代表本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
grossness, grosso modo, grossout, grossular, grossularite, grosul, grosvener siraitia, Grosvenor, grosz, groszy,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据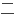
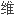
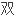调和方程的特点并借助于MATHEMATICA软件,得到了应力函数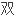调和方程的多项式解。
声明：以上例句、词性分类均由互联网资源自动生成，部分未经过人工审核，
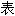
内容亦不代本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
grotty, grouch, grouchily, grouchy, ground, ground ball, ground bass, ground beetle, ground cherry, ground control,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据二维双调和方程的特点并借助于MATHEMATICA软件,得到了
数双调和方程的多项式解。
声明：以上例句、词性分类均
网资源自动生成，部分未经过人工审核，其表达内容亦不代表本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
ground rule, ground speed, ground squirrel, ground state, ground stroke, ground substance, ground swell, ground tackle, ground water, ground wave,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,
diào hé de
conciliatory, consistent, consonant, symphoniousAccording to the nature of two-dimensional biharmonic equations,this paper obtains a polynomial solution of the biharmonic equation for stress function by means of the MATHEMATICA software.
根据二维双调和方程的特点并借助于MATHEMATICA软件,
到了应力函数双调和方程的多项式解。
声明：以上例句、词性分类均由互联网资
生成，部分未经过人工审核，其表达内容亦不代表本软件的观点；若发现问题，欢迎向我们指正。
用户正在搜索
groundfire, groundfish, ground-glass-like, groundhog, Groundhog Day, grounding, groundkeeper, groundless, ground-level, groundline,
相似单词
调号, 调合, 调合的, 调合物, 调和, 调和的, 调和地, 调和化, 调和物, 调和主义者,